Integrales para el cálculo de áreas de figuras planas (II)

Acabé la anterior entrada proponiendo realizar el mismo procedimiento de cálculo de área con otra figura, la Lemniscata de Bernoulli.

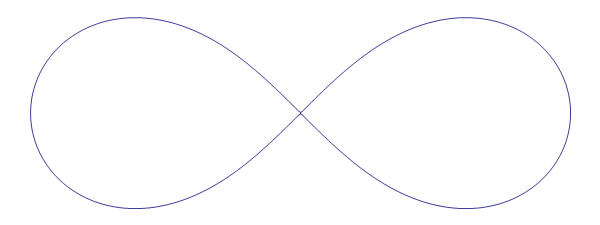
(x²+y²)² = a·(x²-y²)

Si lo habéis intentado os habréis topado con algunas dificultades, comparado con el procedimiento realizado con la elipse. En el caso de la elipse pudimos despejar fácilmente la variable "y" de la ecuación cartesiana implícita, pero en el caso de la lemniscata no resulta tan sencillo. Aunque se puede realizar, y obtenemos las funciones:

De manera análoga a lo que hicimos con la elipse, como la lemniscata tiene ejes de simetría en los ejes OX y OY, podemos calcular la integral de la función positiva anterior. Pero para ello debemos hallar una primitiva de la función.

Bueno, no parece una tarea sencilla. Sin embargo, afortunadamente tenemos otros métodos (no incluidos en el temario de 2º de Bachillerato, sino en la formación universitaria) para calcular el área encerrada por una curva. Recurrimos a las integrales dobles:

Gracias al teorema de Green, si la curva cumple unas determinadas condiciones, podemos transformar la integral doble anterior en una integral de contorno:

(Nota: también existen otras expresiones equivalentes para calcular el área)

¿Cómo nos facilita todo lo anterior el cálculo del área? Pues si conocemos una ecuación paramétrica del contorno, podemos calcular el área como una integral de línea que se transforma en una integral simple:

En nuestro ejemplo de la Lemniscata de Bernoulli, conocemos sus ecuaciones paramétricas (0 <= t < 2·pi):

Teniendo en cuenta que la lemniscata es simétrica respecto al eje OY, calculamos el área de uno de los trozos de la lemniscata que forma una curva cerrada simple, de la siguiente manera:

Por tanto, el área de la Lemniscata de Bernoulli es igual a a² unidades cuadradas.

Podríamos haber utilizado las ecuaciones paramétricas de la elipse (0 <= t < 2·pi)

x = a·cos(t)

y = a·sen(t)

para calcular el área con este procedimiento y obtendríamos:

En la próxima entrada explicaré lo que podemos hacer cuando conocemos la ecuación polar del contorno de la figura de la que queremos calcular su área.