Crónicas nicaragüenses: curso de formación a docentes

Entrada publicada el 20 de septiembre de 2011 en la web de la SBM-XEIX.

El pasado mes de julio (2011) participé en un proyecto de cooperación con el objetivo de formar docentes en activo del departamento de Madriz (Nicaragua). Este proyecto tiene una duración inicial de 3 años y está coordinado por la UIB, la UNAN-Leon y la UCOM. El año pasado, que fue el primero, se trataron varios temas como, por ejemplo, didáctica general, currículum y organización de centro. Este año se ha tratado la formación en didácticas específicas y me ofrecieron encargarme de uno de los módulos de Didáctica de las Matemáticas.

Desde aquí quiero reiterar mi agradecimiento por haberme ofrecido esta oportunidad tan enriquecedora tanto a nivel profesional como personal. Por otra parte, también ha sido todo un placer compartir este proyecto con el equipo de profesores y becarias de la UIB (y CEP de Palma), que me han demostrado ser una maravillosas personas.

Equipo de la UIB

He encontrado que puede ser interesante contaros la experiencia del curso de formación con los docentes nicaragüenses, así que a continuación hago un resumen del desarrollo de las cuatro sesiones que hicimos en la parte presencial (16h) del curso.

Sesión 1:

La primera parte de esta sesión la dedicamos a presentarnos todos los asistentes con datos básicos como el nombre, el centro educativo y el nivel y cursos en los que se imparte docencia. A continuación se pidió por escrito a los asistentes que describieran sus expectativas en cuanto al curso y qué contenidos les gustaría que se trataran.

Después de aclarar y consensuar algunos aspectos de los contenidos y objetivos del curso, se pasó un test anónimo a los asistentes en el que se trataban varias cuestiones referentes a las creencias y concepciones de los docentes respecto a las matemáticas y su enseñanza para comenzar a abrir el debate.

Una vez hecho esto, se pidió que apuntasen en el dossier cómo son sus clases de matemáticas, describiendo una sesión de un tema cualquiera. El objetivo de esta actividad era reflexionar sobre la propia práctica docentes y, en las siguientes actividades, comparar esta práctica con la que dice la legislación y algunos de los marcos teóricos de la Didáctica de las Matemáticas.

Por tanto, la siguiente actividad consistió en leer fragmentos de la legislación educativa de Nicaragua, que había seleccionado previamente, para debatir sobre estos aspectos y compararlos con lo que se había puesto en la actividad anterior. Los asistentes respondieron interesados y sorprendió que ninguno se había leído nunca estos documentos (la mayoría ni conocía su existencia).

En la última parte de la se realizó una actividad en el patio de la sede universitaria con el objetivo de mostrar un ejemplo de cómo se pueden llevar a cabo muchas de las cuestiones innovadoras que aparecieron en los textos y los debates.

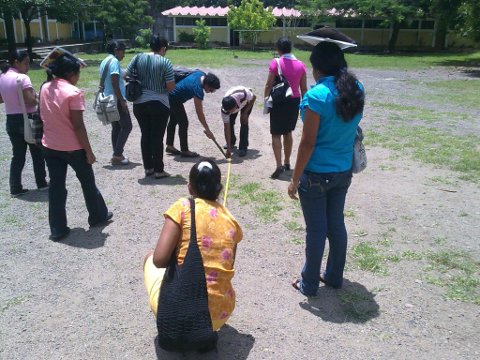Docentes nicaragüenses trabajando en el patio

En esta actividad se trataron contenidos matemáticos como la medida, unidades de medida (convencionales y no convencionales) y conversión, la estimación, los números decimales y sus operaciones, las figuras planas, las aproximaciones, ... Pude constatar en esta sesión que la mayoría de los docentes presentan deficiencias graves de conocimientos básicos en la materia.

La actividad se había planificado convenientemente para que salieran contenidos variados. Este era uno de los objetivos y mostraba una de las recomendaciones metodológicas que había aparecido antes: la interconexión de los contenidos. Otras cuestiones metodológicas que se ejemplificaron con esta actividad fueron: el papel del docente como guía del proceso sin dar directamente las soluciones a los problemas que surgen, el papel activo del alumno, la conexión de los contenidos con la vida real, la interrelación entre alumnos, la realización de actividades abiertas, ...

A los docentes les gustó mucho esta actividad.

Sesión 2:

Esta sesión comenzó con la lectura y reflexión de un documento que facilité en el que se explicaban los principios metodológicos de la Educación Matemática Realista, un marco de referencia para poder analizar y planificar la docencia de la asignatura de Matemáticas. Se explicaron estos principios con ejemplos de actividades que mostraban la aplicación de los mismos y gran parte de la sesión se dedicó a mostrar cómo podemos transformar poco a poco las actividades que hacen los docentes en sus clases en actividades que incluyan los aspectos metodológicos tratados. Por ejemplo, tratamos cómo podemos transformar una actividad cerrada sin contexto en una actividad abierta con contexto.

Se leyó y debatió también un documento en el que una profesora de matemáticas, que lleva a su hijo a una escuela en la que la enseñanza de las matemáticas se basa en el aprendizaje de los algoritmos estándar de las operaciones básicas de una manera mecánica y cerada, relata el cambio que se produce en su hijo cuando lo cambian a otra escuela con metodologías más abiertas y en la que dejan que los niños sigan sus estrategias personales para realizar las operaciones. Este texto también inició el debate sobre la enseñanza de las matemáticas basada en algoritmos estándar cerrados como un producto final de otros que los alumnos deben aprender sin entender los fundamentos de su funcionamiento. También se trataron diversas estrategias personales para el cálculo mental.

Para acabar la sesión se hizo una actividad que ejemplifica el denominado principio de reinvención guiada en el que se ve cómo el alumno, con la guía del profesor, es quien redescubre los contenidos como contraposición a una enseñanza en la que es el profesor que muestra los contenidos a los alumnos.

Actividad de construcción de poliedros y reinvención de la fórmula de Euler

Aprovechando que uno de los temas que surgió (y que pude detectar como una deficiencia grave) es el acceso casi inexistente a recursos para utilizar en el aula, se hizo esta actividad con objetos del entorno: llevé al aula palillos y chucherías (que perfectamente se pueden substituir por palos y barro en caso de no tener acceso a ellos) para construir poliedros. A partir de las construcciones que hicieron los asistentes iba realizando preguntas y proponiendo problemas de manera dirigida para que fueran ellos los que llegasen al resultado de la propiedad buscada: la fórmula de Euler para los poliedros.

Sesión 3:

Comenzamos esta sesión mostrando, debatiendo y ejemplificando otras propuestas metodológicas que  quedaron pendientes en la sesión anterior como, por ejemplo, las situaciones de investigación en el aula de matemáticas y cómo aprovechar cualquier duda e inquietud que surge de los alumnos para poder hacer este tipo de actividades.

Después comenzamos a hablar de otro tema fundamental dentro de la enseñanza de las matemáticas: la resolución de problemas. La discusión surgió en sesiones anteriores, pero en esta tratamos de una manera más explícita qué entendemos por problema e introdujimos la diferencia entre lo que consideramos un ejercicio y lo que consideramos un problema. A continuación tratamos las fases de la la resolución de problemas de George Polya y debatimos diversas propuestas metodológicas que puede realizar el docente en cada fase para ayudar a los alumnos a ser más competentes en la resolución de problemas.

Durante una de las sesiones de trabajo

Aprovechando que uno de los docentes contó que hacía poco que una alumna le planteó un problema en clase, lo propuse a todo el grupo para poder ejemplificar muchos de los aspectos debatidos. Casualmente, el problema que propusieron no tenía solución (o mejor dicho, la solución del problema era decir que es imposible conseguir la situación que se buscaba), hecho que fue muy bien para tratar otro tema que surgió en la sesión anterior: no proponer siempre problemas con una única solución "bonita" y preparada, sino también proponer problemas con múltiples soluciones o, como era el caso, problemas "sin solución". Por tanto, una vez que justifiqué que no era posible encontrar una solución al problema propuesto (ningún docente intentó razonar que no era posible y todos emplearon el tiempo en buscar posibles soluciones), hice modificaciones al problema, creando otros que proponía a la clase como nuevas situaciones de investigación. De esta manera se mostró también como, aprovechando un problema que ha surgido de la clase, podemos modificar las condiciones de este para dirigirlo hacia otros contenidos que nos puedan interesar en un determinado momento.

Finalmente, para acabar esta sesión, como el primer día algunos de los docentes manifestaron su interés por conocer recursos lúdicos, se explicaron algunos juegos para realizar en clase de matemáticas: trucos de matemagia, cartas, dominó, bingo, ...

Sesión 4:

Desde la segunda sesión dedicaba tiempo de clase a que los docentes anotaran en una hoja aquellas cuestiones y propuestas que se trataban en el curso y que encontraran que podían ir incluyendo en su práctica diaria de aula. Esta sesión se dedicó a hacer un listado conjunto de todas aquellas cosas que habían apuntado y añadir aquello que encontraran que era interesante.

Una vez que dimos por terminada esta lista, expliqué en qué consistía la parte no presencial del curso, la aplicación al aula: coger de esta lista los elementos que cada docente considere que puede incorporar a su práctica docente, realizar una planificación de una unidad didáctica con estas innovaciones, después llevarla al aula y redactar una memoria de cómo ha ido la experiencia para enviármela.

Foto de grupo en la última sesión de trabajo presencial

Finalmente, antes de salir al acto de clausura, se repartió a los docentes los mismos tests de creencias y concepciones sobre las matemáticas y su enseñanza que se pasaron el primer día. Esto me permite comprobar si se ha producido o no cierto progreso en los docentes asistentes al curso. Para acabar, se rellenaron los cuestionarios de evaluación del curso.

En el acto de clausura los docentes de mi grupo me mostraron su agradecimiento en forma de regalo: un cuadro de artesanía local.

Obsequio de los docentes nicaragüenses

Conclusiones personales:

Este tipo de proyectos de cooperación, además de muy necesarios y útiles para el desarrollo de la educación de un país como Nicaragua, considero que son insuficientes en cuanto a la duración y a la población de docentes a la que llega esta formación básica. Debemos tener presente la situación desde la que partimos, que las cosas no cambian nunca de un día para otro y que este proyecto tiene una serie de limitaciones, pero que al mismo tiempo inicia un camino seguramente muy provechoso, incluso con repercusiones en las administraciones competentes.

Por otra parte, este proyecto también ha servido para detectar necesidades y deficiencias de los docentes nicaragüenses como, por ejemplo, la imposibilidad de la mayoría de ellos de acceder a libros para poder formarse y actualizar sus conocimientos (que en algunos casos son muy pobres) o encontrar recursos para poder utilizar en sus clases. Desde mi punto de vista, esto es una deficiencia muy grave y deberían dirigirse muchos de los esfuerzos en este sentido. Seguramente es inimaginable el abanico de posibilidades que abriría que (por lo menos) los docentes tuvieran un acceso decente a Internet y una formación en cómo utilizarla con fines auto-formativos y educativos.

¡Aún queda trabajo por hacer!